plotypus.preprocessing module

Light curve space transformation preprocessors for regressing upon.

class plotypus.preprocessing.Fourier(degree=3, degree_range=None, regressor=LinearRegression(copy_X=True, fit_intercept=False, n_jobs=1, normalize=False))[source]

Bases: object

Transforms observed data from phase-space to Fourier-space.

In order to represent a light curve as a Fourier series of the form

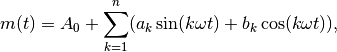
m(t) = A_0 + \sum_{k=1}^n (a_k \sin(k \omega t) + b_k \cos(k \omega t)),

phased time observations are transformed into a design matrix 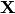\mathbf{X} by Fourier.design_matrix(), such that linear regression can be used to solve for coefficients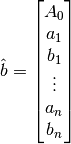

\hat{b} = \begin{bmatrix} A_0 \\ a_1 \\ b_1 \\ \vdots \\ a_n \\ b_n \end{bmatrix}

in the matrix equation

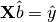
\mathbf{X} \hat{b} = \hat{y}

where 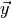\vec{y} is the vector of observed magnitudes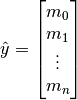

\hat{y} = \begin{bmatrix} m_0 \\ m_1 \\ \vdots \\ m_n \end{bmatrix}

If degree_range is not None, degree is selected via baart_criteria(). Otherwise the provided degree is used.

Parameters

degree
: positive int, optional
Degree of Fourier series to use, assuming degree_range is None (default 3).
degree_range
: 2-tuple or None, optional
Range of allowed degrees to search via baart_criteria(), or None if single provided degree is to be used (default None).
regressor
: object with “fit” and “transform” methods, optional
Regression object used for fitting light curve when selecting degree via baart_criteria(). Not used otherwise (default sklearn.linear_model.LinearRegression(fit_intercept=False)).
baart_criteria(X, y)[source]

Returns the optimal Fourier series degree as determined by Baart’s Criteria [JOP].

Citations

[JOP]J. O. Petersen, 1986, “Studies of Cepheid type variability. IV. The uncertainties of Fourier decomposition parameters.”, A&A, Vol. 170, p. 59-69
static baart_tolerance(X)[source]

Returns the autocorrelation cutoff of X for baart_criteria(), as given by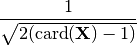

\frac{1}{\sqrt{2 (\operatorname{card}(\mathbf{X}) - 1)}}

Parameters

X
: array-like, shape = [n_samples, 1]
Column vector of phases

Returns

static design_matrix(phases, degree)[source]

Constructs an 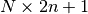N \times 2n+1 matrix of the form: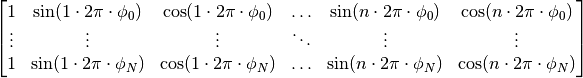

\begin{bmatrix} 1 & \sin(1 \cdot 2\pi \cdot \phi_0) & \cos(1 \cdot 2\pi \cdot \phi_0) & \ldots & \sin(n \cdot 2\pi \cdot \phi_0) & \cos(n \cdot 2\pi \cdot \phi_0) \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & \sin(1 \cdot 2\pi \cdot \phi_N) & \cos(1 \cdot 2\pi \cdot \phi_N) & \ldots & \sin(n \cdot 2\pi \cdot \phi_N) & \cos(n \cdot 2\pi \cdot \phi_N) \end{bmatrix}

where 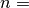n = degree, 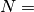N = n_samples, and 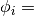\phi_i = phases[i].

phases : array-like, shape = [n_samples]

fit(X, y=None)[source]

Sets self.degree according to baart_criteria() if degree_range is not None, otherwise does nothing.

Parameters

X
: array-like, shape = [n_samples, 1]
Column vector of phases.
y
: array-like or None, shape = [n_samples], optional
Row vector of magnitudes (default None).

Returns

self : returns an instance of self

static fourier_ratios(phase_shifted_coeffs)[source]

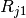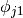Returns the R_{j1} and \phi_{j1} values for the given phase-shifted coefficients.

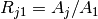
R_{j1} = A_j / A_1

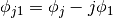
\phi_{j1} = \phi_j - j \phi_1

Parameters

phase_shifted_coeffs
: array-like, shape = [2n+1]
Fourier sine or cosine series coefficients. [ A_0, A_1, \Phi_1, \ldots, A_n, \Phi_n ].

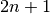Returns

out
: array-like, shape = [2n+1]
Fourier ratios [ R_{21}, \phi_{21}, \ldots, R_{n1}, \phi_{n1} ].
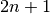get_params(deep=False)[source]

Get parameters for this preprocessor.

Parameters

deep
: boolean, optional
Only here for scikit-learn compliance. Ignore it (default False).

Returns

params
: dict
Mapping of parameter name to value.
static phase_shifted_coefficients(amplitude_coefficients, form='cos', shift=0.0)[source]

Converts Fourier coefficients from the amplitude form to the phase-shifted form, as either a sine or cosine series.

Amplitude form:

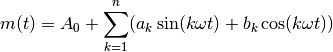
m(t) = A_0 + \sum_{k=1}^n (a_k \sin(k \omega t) + b_k \cos(k \omega t))

Sine form:

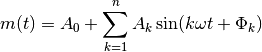
m(t) = A_0 + \sum_{k=1}^n A_k \sin(k \omega t + \Phi_k)

Cosine form:

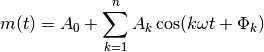
m(t) = A_0 + \sum_{k=1}^n A_k \cos(k \omega t + \Phi_k)

Parameters

amplitude_coefficients
: array-like, shape = [2n+1]
Array of coefficients [ A_0, a_1, b_1, \ldots a_n, b_n ].
form
: str, optional
Form of output coefficients, must be one of ‘sin’ or ‘cos’ (default ‘cos’).
shift
: number, optional
Shift to apply to light curve (default 0.0).

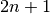Returns

out
: array-like, shape = [2n+1]
Array of coefficients [ A_0, A_1, \Phi_1, \ldots, A_n, \Phi_n ].
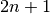set_params(**params)[source]

Set parameters for this preprocessor.

Returns

self : returns an instance of self

transform(X, y=None, **params)[source]

Transforms X from phase-space to Fourier-space, returning the design matrix produced by Fourier.design_matrix() for input to a regressor.

Parameters

X
: array-like, shape = [n_samples, 1]
Column vector of phases.
y
: None, optional
Unused argument for conformity (default None).

Returns

design_matrix
: array-like, shape = [n_samples, 2*degree+1]
Fourier design matrix produced by Fourier.design_matrix().